Question

【题目】如图，在边长为4的正方形ABCD中，对角线AC，BD相交于点O，点E是AD边上一点，连接CE，把△CDE沿CE翻折，得到△CPE，EP交AC于点F，CP交BD于点G，连接PO，若PO∥BC，则四边形OFPG的面积是_____．

Answer 1

【答案】8﹣4

【解析】

先过P作PM⊥AO于M，作PN⊥BO于N，延长PO交CD于H，根据△CDO是等腰直角三角形，运用勾股定理求得PH==2，得到PO=PH-OH=2-2，进而得到正方形PMON的面积=OP2=8-4，最后判定△PMF≌△PNG（ASA），得出S△PMF=S△PNG，根据S四边形OFPG=S正方形PMON，即可得出四边形OFPG的面积是8-4

如图所示，过P作PM⊥AO于M，作PN⊥BO于N，延长PO交CD于H，

∵PO∥BC，BC⊥CD，

∴PH⊥CD，

又∵△CDO是等腰直角三角形，

∴OH=CD=2=CH，OH平分∠COD，

由折叠可得，CP=CD=4，

∴Rt△PCH中,PH==2，

∴PO=PHOH=22，

∵PO平分∠AOB，PM⊥AO，PN⊥BO，

∴PM=PN，

矩形PMON是正方形，

∴正方形PMON的面积=OP2=(22)2=84，

∵∠FPG=∠MON=90°，

∴∠FPM=∠GPN，

在△PMF和△PNG中，

，

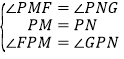∴△PMF≌△PNG(ASA)，

∴S△PMF=S△PNG，

∴S四边形OFPG=S正方形PMON，

∴四边形OFPG的面积是84，

故答案为：84