��Ŀ����
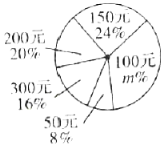
����Ŀ���������۵�ӱ�����ÿ��0.30Ԫ���һ�����������۵������ļ۸�Ϊ0.50Ԫ��Լ���������ı�ֽ�����˻������磬�˻���Ǯ��y��Ԫ�����˻��ı�ֽ����k���ݣ�֮��ĺ�����ϵʽ���£���0��k��30ʱ�� y��![]() ����k��30ʱ��y��0.02k���־��г����鷢�֣���һ�����У���30���������20�������150��/�죬��10��ֻ������100��/�죬������涨ÿ��������̯��ı�ֽ������������ͬ��
����k��30ʱ��y��0.02k���־��г����鷢�֣���һ�����У���30���������20�������150��/�죬��10��ֻ������100��/�죬������涨ÿ��������̯��ı�ֽ������������ͬ��
��1�����üұ���̯��ÿ��ӱ�������ı�ֽ��x�ݣ�����100<x��150������ë����ΪWԪ����W����x�ĺ�����ϵʽ��
��2����������ٱ�ֽʱ����ë�������Ϊ���٣���ע����ë����=�������۶�-���ܳɱ�����
���𰸡���1��W=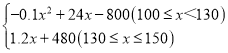 ����2�������150�ݱ�ֽʱ����ë�������Ϊ660Ԫ��
����2�������150�ݱ�ֽʱ����ë�������Ϊ660Ԫ��
��������
��1���������⣬���õ�100��x��130ʱ����130��x��150ʱ��������ë����=�������۶�-���ܳɱ��ֱ�ó����ɣ�
��2���ֱ𣬵�100��x��130ʱ����130��x��150ʱȥ�������ֱ���ø��ε����ֵ���̶���øüұ���̯��ÿ��ӱ���������ٷݱ�ֽ����ʹÿ������ë���������������Ǯ����
��1����100��x��130ʱ��
W=20��0.5��x+10��0.5��100+10��[![]() ��x-100��2+
��x-100��2+![]() ��x-100��]-0.3x��30
��x-100��]-0.3x��30
=-0.1x2+24x-800
��130��x��150ʱ��
w=20��0.5��x+10��0.5��100+10[0.02��x-100��]-0.3x��30
=1.2x+480��
��W=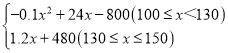
��2����100��x��130ʱ��
w=-0.1x2+24x-800 =-0.1��x-120��2+640��
�൱x=120ʱ��W���=640��
��130��x��150ʱ��
w=1.2x+480��
��1.2��0��
��W��x�����������
��x=150ʱ��W���=660��
660��640
���������������150�ݱ�ֽʱ����ë�������Ϊ660Ԫ��