题目内容
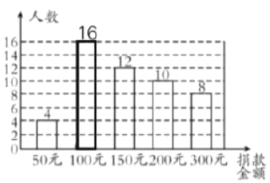
【题目】为了能够帮助武汉疫情,某公司通过武汉市慈善总会二维码给武汉捐款,根据捐款情况制成不完整的扇形统计图(图1)、条形统计图(图2).
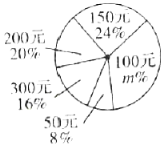

图1 图2
(1)根据以上信息可知参加捐款总人数为______,![]() ______,捐款金额中位数为______,请补全条形统计图;
______,捐款金额中位数为______,请补全条形统计图;
(2)若从捐款的人中,随机选一人代表公司去其它公司做捐款宣传,求选中捐款不低于![]() 元的人的概率;
元的人的概率;
(3)若其它公司有几人参与了捐款活动,把新捐款数与原捐款数合并成一组新数据,发现众数发生改变,请求出至少有几人参与捐款.
【答案】(1)50,32,150,条形统计图见解析;(2)![]() ;(3)4人.
;(3)4人.
【解析】
(1)用捐款150元频数除以频率,求出捐款总人数为50,用总人数减去已知四组频数,再除以总人数,即可求出m,根据各项数据,补全条形统计图,求出第25、26个数据,即可求出中位数;
(2)求出捐款不低于![]() 元人数的频率,用频率估计概率即可;
元人数的频率,用频率估计概率即可;
(3)结合统计图,现众数为16,故至少要4人参与捐款,且捐款数均为150元,才能改变众数.
解:(1)捐款总人数为![]() ;
;
捐款为100元人数为![]() 所占百分比为
所占百分比为![]() ,
,
∴m=32;
本次捐款共50人参加,按捐款数从低到高排序,第25、26个数为150,150,
故中位数为![]() ,
,
补全条形统计图如下:
 ;
;
(2)![]() ;
;
(3)至少![]() 人参与捐款.
人参与捐款.
![]() 原数据众数为
原数据众数为![]() 元,
元,
若至少增加![]() 人,每人捐款
人,每人捐款![]() 元,
元,
则新众数为![]() 元和
元和![]() 元,
元,
![]() 至少增加
至少增加![]() 人.
人.

练习册系列答案
相关题目