题目内容
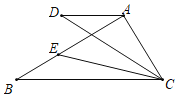
【题目】如图,AD∥BC,CE平分∠BCD,∠DAC=3∠BCD,∠ACD=20°,当AB与AC互相垂直时,∠B的度数为_____.
【答案】30°
【解析】
由平行线的性质得∠DAC+∠BCA=180°,构建方程x+3x+20°=180°,解得x=40°,再根据垂直的定义,余角的性质求出∠B的度数为30°.
解:设∠BCD=x,如图所示:
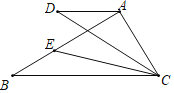
∵∠DAC=3∠BCD,
∴∠DAC=3x,
又∵AD∥BC,
∴∠DAC+∠BCA=180°,
又∵∠BCA=∠BCD+∠ACD,
∠ACD=20°,
∴x+3x+20°=180°,
解得:x=40°,
∴∠BCA=60°,
又∵AB⊥AC,
∴∠BAC=90°,
又∵∠B+∠BAC=90°,
∴∠B=30°,
故答案为30°.

练习册系列答案
相关题目