Question

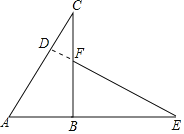
【题目】如图，△ABC是直角三角形，延长AB到点E，使BE＝BC，在BC上取一点F，使BF＝AB，连接EF，△ABC旋转后能与△FBE重合，请回答：

(1)旋转中心是点______，旋转的最小角度是______度

(2)AC与EF的位置关系如何，并说明理由。

Answer 1

【答案】（1）点B，90；（2）AC⊥EF 理由见解析.

【解析】试题分析：（1）由条件易得BC和BE，BA和BF为对应边，而△ABC旋转后能与△FBE重合，于是可判断旋转中心为点B；根据旋转的性质得∠ABF等于旋转角，从而得到旋转角度；

（2根据旋转的性质即可判断AC=EF，AC⊥EF．

试题解析：（1）∵BC=BE，BA=BF，

∴BC和BE，BA和BF为对应边，

∵△ABC旋转后能与△FBE重合，

∴旋转中心为点B；

∵∠ABC=90°，

而△ABC旋转后能与△FBE重合，

∴∠ABF等于旋转角，

∴旋转了90度，

故答案为：B，90；

（2）AC⊥EF理由如下：

延长EF交AC于点D由旋转可知∠C=∠E

∵∠ABC=90°

∴∠C+∠A=90°

∴∠E+∠A=90°

∴∠ADE=90°

∴AC⊥EF．