Question

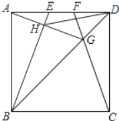
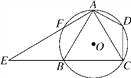
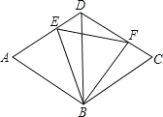
【题目】如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点)，且AE+CF=2，则线段EF长的最小值是__________.

Answer 1

【答案】

【解析】

由在边长为2的菱形ABCD中，BD=2，易得△ABD、△CBD都是边长为2的正三角形，继而证得△BDE≌△BCF（SAS），继而证得△BEF是正三角形，继而可得当动点E运动到点D或点A时，BE的最大，当BE⊥AD，即E为AD的中点时，BE的最小．

∵四边形ABCD是边长为2的菱形，BD＝2，
∴△ABD、△CBD都是边长为2的正三角形，
∵AE＋CF＝2，
∴CF＝2AE＝ADAE＝DE，
又∵BD＝BC＝2,∠BDE＝∠C＝60，
DE＝DF,∠BDE＝∠C,BD＝BC，
∴△BDE≌△BCF(SAS)，
∴∠EBD＝∠FBC，
∴∠EBD＋∠DBF＝∠FBC＋∠DBF，
∴∠EBF＝∠DBC＝60，
又∵BE＝BF，
∴△BEF是正三角形，
∴EF＝BE＝BF，
当BE⊥AD,即E为AD的中点时,BE的最小值为,

所以EF＝BE＝.