题目内容
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n= ![]() .
.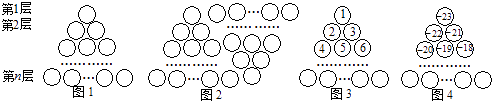
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
﹣23,﹣22,﹣21,﹣20,…,则所有圆圈中各数之和为 .
【答案】61;627
【解析】解:第10层最后一个数为:10(10+1)÷2=55,所以第11层中间一个数为:55+6=61,
图4中所有圆圈的个数为:1+2+3+…+11=11(11+1)÷2=66个数,其中23个负数,1个0,42个正数,
所以图4中所有圆圈中各数之和=﹣23﹣22﹣21…﹣1+0+1+2+…+42=(1+2+3+…+42)﹣(1+2+3+…+23)=42(42+1)÷2﹣23(23+1)÷2=903﹣276=627.
所以答案是:61;627.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
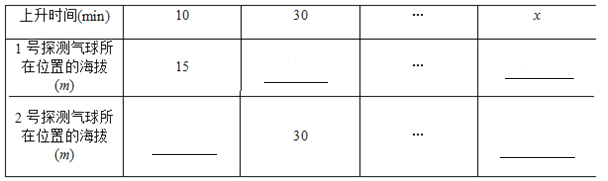
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.