题目内容
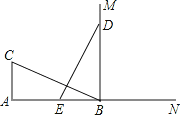
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC. 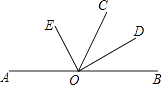
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
【答案】
(1)解:∵OE、OD分别平分∠AOC、∠BOC,
∴∠EOC= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,
∠BOC,
∴∠EOD=∠EOC+∠COD= ![]() ∠AOC+
∠AOC+ ![]() ∠BOC=
∠BOC= ![]() ∠AOB,
∠AOB,
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD= ![]() ∠AOB=90°
∠AOB=90°
(2)解:∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°﹣∠AOC=80°
【解析】(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC= ![]() ∠AOC,∠COD=
∠AOC,∠COD= ![]() ∠BOC,进而得出∠EOD=∠EOC+∠COD=
∠BOC,进而得出∠EOD=∠EOC+∠COD= ![]() ∠AOB=90°;(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
∠AOB=90°;(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线).

练习册系列答案
相关题目