题目内容
【题目】1号探测气球从海拔5 m处出发,以l m/min的速度上升.与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升,两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50).
(1)根据题意,填写下表:
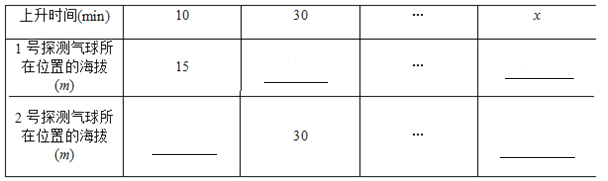
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
【答案】(1)20,35,x+5,0.5x+15;(2)此时气球上升了20 min,都位于海拔25 m的高度.(3)15 m.
【解析】试题分析:(Ⅰ)由题意可得,1号探测气球从海拔5 m处出发,以1m/min的速度上升,30min时1号探测气球的海拔高度为35m,xmin时海拔高度为(x+5)m;2号探测气球从海拔15m处出发,以0.5m/min的速度上升,10min时2号探测气球的海拔高度为20m,xmin时海拔高度为(0.5x+15)m.
(Ⅱ)令x+5=0.5x+15,若x有解且x的值位于0≤x≤50这个范围,则说明在某时刻两个气球能位于同一高度,这时求得x的值再带入求气球的海拔高度即可,若x有解且x的值不位于0≤x≤50这个范围,则不存在某时刻两个气球位于同一高度.
(Ⅲ)当30≤x≤50时,由题意,可知1号气球所在位置的海拔始终高于2号气球,设两个气球在同一时刻所在位置的海拔相差有y米,用x表示出y,根据所得的关系式及x的取值范围,即可求得两个气球所在位置的海拔高度相差的最大值.
试题解析:(Ⅰ)35,x+5;20,0.5x+15.
(Ⅱ)两个气球能位于同一高度.
根据题意,x+5=0.5x+15,解得x=20.
有x+5=25.
答:此时,气球上升了20min,都位于海拔25m的高度.
(Ⅲ))当30≤x≤50时,
由题意,可知1号气球所在位置的海拔始终高于2号气球,
设两个气球在同一时刻所在位置的海拔相差有y米,
则y=(x+5)—(0.5x+15)=0.5x—10.
∵0.5>0,
∴y随x的增大而增大.
∴当x=50时,y取得最大值15.
答:两个气球所在位置的海拔最多相差15米.

 阅读快车系列答案
阅读快车系列答案