题目内容
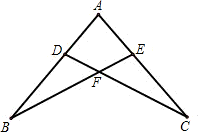 如图所示,AB=AC,要说明△ADC≌△AEB,需添加的条件不能是
如图所示,AB=AC,要说明△ADC≌△AEB,需添加的条件不能是
- A.∠B=∠C
- B.AD=AE
- C.∠ADC=∠AEB
- D.DC=BE
D
分析:△ADC和△AEB中,已知的条件有AB=AC,∠A=∠A;要判定两三角形全等只需条件一组对应角相等,或AD=AE即可.可据此进行判断,两边及一边的对角相等是不能判定两个三角形全等的.
解答:A、当∠B=∠C时,符合ASA的判定条件,故A正确;
B、当AD=AE时,符合SAS的判定条件,故B正确;
C、当∠ADC=∠AEB时,符合AAS的判定条件,故C正确;
D、当DC=BE时,给出的条件是SSA,不能判定两个三角形全等,故D错误;
故选D.
点评:本题主要考查的是全等三角形的判定方法,需注意的是SSA和AAA不能作为判定两个三角形全等的依据.
分析:△ADC和△AEB中,已知的条件有AB=AC,∠A=∠A;要判定两三角形全等只需条件一组对应角相等,或AD=AE即可.可据此进行判断,两边及一边的对角相等是不能判定两个三角形全等的.
解答:A、当∠B=∠C时,符合ASA的判定条件,故A正确;
B、当AD=AE时,符合SAS的判定条件,故B正确;
C、当∠ADC=∠AEB时,符合AAS的判定条件,故C正确;
D、当DC=BE时,给出的条件是SSA,不能判定两个三角形全等,故D错误;
故选D.
点评:本题主要考查的是全等三角形的判定方法,需注意的是SSA和AAA不能作为判定两个三角形全等的依据.

练习册系列答案
相关题目
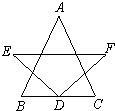 33、如图所示,AB=AC,D是BC的中点,DE=DF,BC∥EF,这个图形是轴对称图形吗?为什么?
33、如图所示,AB=AC,D是BC的中点,DE=DF,BC∥EF,这个图形是轴对称图形吗?为什么? 4、如图所示,AB=AC,∠A=40°,AB的垂直平分线MN交AC与D,则∠DBC=( )
4、如图所示,AB=AC,∠A=40°,AB的垂直平分线MN交AC与D,则∠DBC=( ) 13、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
13、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=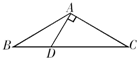 19、如图所示,AB=AC,∠B=30°,AD⊥AC,求∠BAD的度数.
19、如图所示,AB=AC,∠B=30°,AD⊥AC,求∠BAD的度数.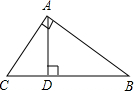 如图所示,AB⊥AC于A,AD⊥BC于D,则图中共有
如图所示,AB⊥AC于A,AD⊥BC于D,则图中共有