题目内容
13、如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=55°
．分析：先证明△ABD≌△ACE（SAS）；再利用全等三角形的性质：对应角相等，求得∠2=∠ABE；最后根据三角形内角与外角的性质即可求出答案．
解答：解：在△ABD与△ACE中，
∵∠1+∠CAD=∠CAE+∠CAD，
∴∠1=∠CAE；
又∵AB=AC，AD=AE，
∴△ABD≌△ACE（SAS）；
∴∠2=∠ABE（对应角相等）；
∵∠3=∠1+∠2，∠1=25°，∠2=30°，
∴∠3=55°．
故填55°．
解：在△ABD与△ACE中，∵∠1+∠CAD=∠CAE+∠CAD，
∴∠1=∠CAE；
又∵AB=AC，AD=AE，
∴△ABD≌△ACE（SAS）；
∴∠2=∠ABE（对应角相等）；
∵∠3=∠1+∠2，∠1=25°，∠2=30°，
∴∠3=55°．
故填55°．
点评：本题考查了全等三角形的判定及性质；解答时，除必备的知识外，还应将条件和所求联系起来，即将所求的角与已知角通过全等及内角、外角之间的关系联系起来．
练习册系列答案
相关题目
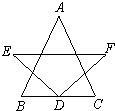33、如图所示，AB=AC，D是BC的中点，DE=DF，BC∥EF，这个图形是轴对称图形吗？为什么？
4、如图所示，AB=AC，∠A=40°，AB的垂直平分线MN交AC与D，则∠DBC=（ ）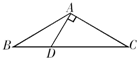
19、如图所示，AB=AC，∠B=30°，AD⊥AC，求∠BAD的度数．
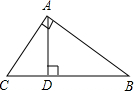如图所示，AB⊥AC于A，AD⊥BC于D，则图中共有