题目内容
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
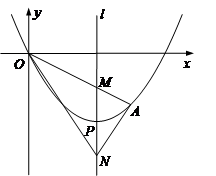
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
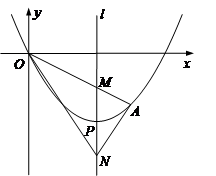
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
(1)
(2)12
(3)相似三角形的基本知识推出该角度的相等,不能

(2)12
(3)相似三角形的基本知识推出该角度的相等,不能
试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为
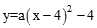 。
。又∵二次函数图象经过原点(0,0),∴
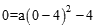 ,解得
,解得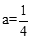 。
。∴二次函数的关系式为
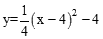 ,即
,即 。(2分)
。(2分)(2)设直线OA的解析式为
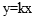 ,将A(6,-3)代入得
,将A(6,-3)代入得 ,解得
,解得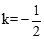 。
。∴直线OA的解析式为
 。
。把x=4代入
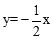 得y=-2。∴M(4,-2)。
得y=-2。∴M(4,-2)。又∵点M、N关于点P对称,∴N(4,-6),MN=4。
∴
 。(3分)
。(3分)(3)①证明:过点A作AH⊥
 于点H,,
于点H,, 与x轴交于点D。则
与x轴交于点D。则设A(
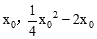 ),
),则直线OA的解析式为
 。
。则M(
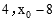 ),N(
),N( ),H(
),H( )。
)。∴OD=4,ND=
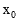 ,HA=
,HA=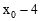 ,NH=
,NH= 。
。∴
 。
。∴

 。∴∠ANM=∠ONM。(2分)
。∴∠ANM=∠ONM。(2分)②不能。理由如下:分三种情况讨论:
情况1,若∠ONA是直角,由①,得∠ANM=∠ONM=450,
∴△AHN是等腰直角三角形。∴HA=NH,即
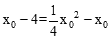 。
。整理,得
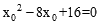 ,解得
,解得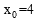 。
。∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
情况2,若∠AON是直角,则
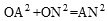 。
。∵
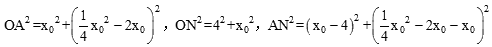 ,
,∴
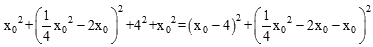 。
。整理,得
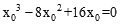 ,解得
,解得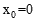 ,
,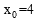 。
。∴此时,故点A与原点或与点P重合。故此时不存在点A,使∠AON是直角。
情况3,若∠NAO是直角,则△AMN∽△DMO∽△DON,∴
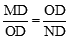 。
。∵OD=4,MD=
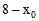 ,ND=
,ND=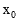 ,∴
,∴ 。
。整理,得
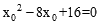 ,解得
,解得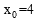 。
。∴此时,点A与点P重合。故此时不存在点A,使∠ONA是直角。
综上所述,当点A在对称轴
 右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)
右侧的二次函数图象上运动时,△ANO不能成为直角三角形。(3分)点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
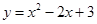 的对称轴为 ( )
的对称轴为 ( )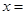 -2
-2 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论: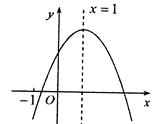
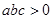 ;②
;②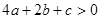 ;③
;③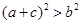 ;
;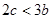 ;⑤
;⑤ 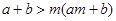 (
(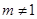 )
) 
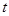 ,△AMN的面积为
,△AMN的面积为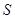 .
.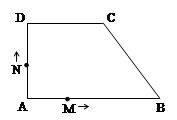

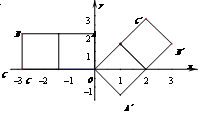
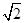 的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.
的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx(a≠0)过点O、B′、C′.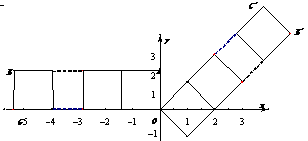

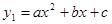 与一次函数
与一次函数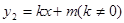 的图像相交于点A(-2,4),B(8,2)。如图所示,则能使
的图像相交于点A(-2,4),B(8,2)。如图所示,则能使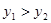 成立的x的取值范围是 。
成立的x的取值范围是 。