题目内容
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
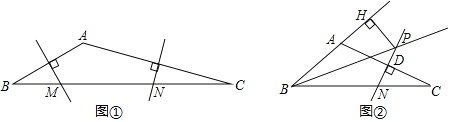
(1)如图①,若BM2+CN2=MN2,则∠BAC= °;
(2)如图②,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H,若AB=4,CB=10,求AH的长.
【答案】(1)135;(2)3;
【解析】
(1)连接AM、AN,由勾股定理的逆定理证出△AMN是直角三角形,∠MAN=90°,证出∠AMN=2∠B,∠ANM=2∠C,得出∠AMN+∠ANM=2(∠B+∠C)=90°,证出∠B+∠C=45°,由三角形内角和定理即可得出答案;
(2)先判断出Rt△APH≌Rt△CPE,进而判断出△BPH≌△BPE,根据全等三角形的性质计算即可得出结论.
解:(1)连接AM、AN,如图①所示:
∵AB、AC边的垂直平分线分别交BC边于点M、N.
∴BM=AM,CN=AN,
∴∠B=∠BAM,∠C=∠CAN,
∵BM2+CN2=MN2,
∴AM2+AN2=MN2,
∴△AMN是直角三角形,∠MAN=90°,
∵∠AMN=∠B+∠BAM,∠ANM=∠C+∠CAN,
∴∠AMN=2∠B,∠ANM=2∠C,
∴∠AMN+∠ANM=2(∠B+∠C)=90°,
∴∠B+∠C=45°,
∴∠BAC=180°﹣(∠B+∠C)=180°﹣45°=135°;
故答案为:135;
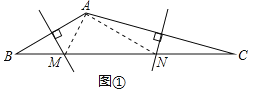
(2)连接AP、CP,过点P作PE⊥BC于点E,如图②所示:
∵BP平分∠ABC,PH⊥BA,PE⊥BC,
∴PH=PE,
∵点P在AC的垂直平分线上,
∴AP=CP,
在Rt△APH和Rt△CPE中,
![]() ,
,
∴Rt△APH≌Rt△CPE(HL)
∴AH=CE,
在△BPH和△BPE中,
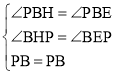 ,
,
∴△BPH≌△BPE(AAS)
∴BH=BE,
∴BC=BE+CE=BH+CE=AB+2AH,
∴AH=![]() (BC﹣AB)=3.
(BC﹣AB)=3.
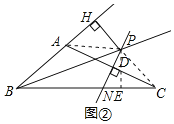

【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为 A、B、C、D 四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩x(分) | 等级 | 人数 |
x≥90 | A | 12 |
75≤x<90 | B | m |
60≤x<75 | C | n |
x<60 | D | 9 |
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中 C 级的圆心角度数;
(3)若该校七年级共有学生 640人,根据抽样结课,估计英语口语达到 B级以上(包括B 级)的学生人数.

【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.




