题目内容
【题目】如图,点C是线段AB上除点A,B外的任意一点,分别以AC,BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:BD=AE.
(2)求证:△NMC是等边三角形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先由△ACD和△BCE是等边三角形,可知AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,故可得出∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,根据SAS定理可知△ACE≌△DCB,然后由全等三角形的性质即可得出结论;
(2)由(1)中△ACE≌△DCB,可知∠CAM=∠CDN,再根据∠ACD=∠ECB=60°,A、C、B三点共线可得出∠DCN=60°,由全等三角形的判定定理可知,△ACM≌△DCN,故MC=NC,再根据∠MCN=60°可知△MCN为等边三角形.
证明:(1)∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,
∵∠DCA=∠ECB=60°,
∴∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE与△DCB中,
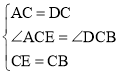 .
.
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵由(1)得,△ACE≌△DCB,
∴∠CAM=∠CDN,
∵∠ACD=∠ECB=60°,而A.C.B三点在同一条直线上,
∴∠DCN=60°,
在△ACM与△DCN中,
∵∠MAC=∠NDC,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴MC=NC,
∵∠MCN=60°,
∴△MCN为等边三角形.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为 A、B、C、D 四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩x(分) | 等级 | 人数 |
x≥90 | A | 12 |
75≤x<90 | B | m |
60≤x<75 | C | n |
x<60 | D | 9 |
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中 C 级的圆心角度数;
(3)若该校七年级共有学生 640人,根据抽样结课,估计英语口语达到 B级以上(包括B 级)的学生人数.






