题目内容
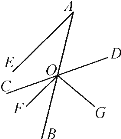
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于点O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
【答案】(1)∠AOD=60°;(2)见解析.
【解析】
(1)根据两直线平行,同位角相等可得∠FOB=∠A=30![]() ,再根据角平分线的定义求出∠COF=∠FOB=30
,再根据角平分线的定义求出∠COF=∠FOB=30![]() ,然后根据平角等于180
,然后根据平角等于180![]() 列式进行计算即可得解;
列式进行计算即可得解;
(2)先求出∠DOG=60![]() ,再根据对顶角相等求出∠AOD=60
,再根据对顶角相等求出∠AOD=60![]() ,然后根据角平分线的定义即可得解.
,然后根据角平分线的定义即可得解.
解:(1)∵AE∥OF,∴∠BOF=∠A=30°,
∵OF平分∠BOC,∴∠COF=∠BOF=30°,∠DOF=180°-∠COF=150°;
(2)由(1)知∠COF=∠BOF=30°,∴∠BOC=60°,∠AOD=∠BOC=60°,
∵OG⊥OF,∴∠BOG=90°-∠BOF=60°,
∴∠DOG=180°-∠BOC-∠BOG=180°-60°-60°=60°,
∴∠AOD=∠DOG=60°,∴OD平分∠AOG.

练习册系列答案
相关题目