题目内容
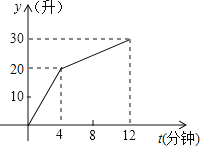
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
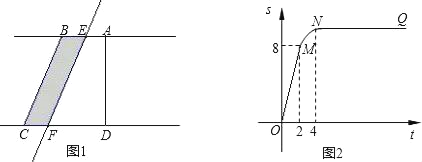
信息读取
(1)梯形上底的长AB= ;
(2)直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
【答案】(1)AB=2.(2)S梯形ABCD=12(3)当平移距离BE大于等于4时,直角梯形ABCD被直线l扫过的面积恒为12(4)S=﹣t2+8t﹣4(5)当t=![]() 或t=4﹣
或t=4﹣![]() 时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
【解析】试题分析:(1)、当点E到达点A时,面积成一次函数,则AB=2;(2)、根图示得出梯形的面积;(3)、根据函数图形得出实际意义;(4)、首先根题意画出图形,然后利用直角梯形的面积减去直角三角形DOF的面积得出函数解析式;(5)、分成0<t<2和2<t<4两种情况分别进行计算.
试题解析:(1)、![]() .
.
(2)、S梯形ABCD="12" .
(3)、当平移距离BE大于等于4时,直角梯形ABCD被直线![]() 扫过的面积恒为12.
扫过的面积恒为12.
(4)、当![]() 时,如下图所示,
时,如下图所示,
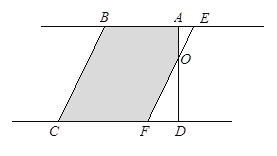
直角梯形ABCD被直线![]() 扫过的面积S=S直角梯形ABCD-SRt△DOF
扫过的面积S=S直角梯形ABCD-SRt△DOF![]() .
.
(5)、①当![]() 时,有
时,有![]() ,解得
,解得![]() .
.
②当![]() 时,有
时,有
![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
答:当![]() 或
或![]() 时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.

练习册系列答案
相关题目