��Ŀ����
����Ŀ����ͼ����![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��ʹ
��ʹ![]() ����һֱ�����ǰ��ֱ�Ƕ�����ڵ�
����һֱ�����ǰ��ֱ�Ƕ�����ڵ�![]() ����
����![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��ֱ��
��ֱ��![]() ���·���
���·���

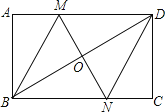
��1����ͼ1�е����ǰ��Ƶ�![]() ��ʱ����ת��ͼ2��ʹһ��
��ʱ����ת��ͼ2��ʹһ��![]() ��
��![]() ���ڲ�����ǡ��ƽ��
���ڲ�����ǡ��ƽ��![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ1�е����ǰ��Ƶ�![]() ��ÿ��5���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���
��ÿ��5���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���![]() ��ʱ��ֱ��
��ʱ��ֱ��![]() ǡ��ƽ�����
ǡ��ƽ�����![]() ����
����![]() ��ֵ��
��ֵ��
��ͼ1�е����ǰ��Ƶ�![]() ��ʱ����ת��ͼ3��ʹһ��
��ʱ����ת��ͼ3��ʹһ��![]() ��
��![]() ���ڲ�����̽��
���ڲ�����̽��![]() ��ֵ��/span>
��ֵ��/span>
���𰸡���1��35������2��11��47����3����AOM-��NOC=20����
��������
��1�����ݽ�ƽ���ߵĶ���ͨ�����㼴����á�BON�Ķ�����
��2����ON�ķ����ӳ���ƽ�֡�AOCʱ������ONƽ�֡�AOCʱ����������ֱ����ۣ����ݽ�ƽ���ߵĶ����Լ��ǵĹ�ϵ���м��㼴�ɣ�
��3�����ݡ�MON=90������AOC=70�����ֱ���á�AOM=90��-��AON����NOC=70��-��AON���ٸ��ݡ�AOM-��NOC=��90��-��AON��-��70��-��AON�����м��㣬���ɵó���AOM���NOC��������ϵ��
�⣺��1����ͼ2�У�
��OMƽ�֡�BOC��
���MOC=��MOB��
�֡ߡ�BOC=110����
���MOB=55����
�ߡ�MON=90����
���BON=��MON-��MOB=35����
��2����2�������������
����ͼ2���ߡ�BOC=110��
���AOC=70����
����ON�ķ����ӳ���ƽ�֡�AOCʱ����AOD=��COD=35����
���BON=35������BOM=55����
����ʱ����ת�ĽǶ�Ϊ55����
������ã�5t=55��
���t=11��
����ͼ3��������ONƽ�֡�AOCʱ����NOA=35����
���AOM=55����
����ʱ����ת�ĽǶ�Ϊ��180��+55��=235����
������ã�5t=235����
���t=47��
����������t=11s��47sʱ��ֱ��ONǡ��ƽ����ǡ�AOC��
�ʴ�Ϊ��11��47��
��3����AOM-��NOC=20����
���ɣ��ߡ�MON=90������AOC=70����
���AOM=90��-��AON����NOC=70��-��AON��
���AOM-��NOC=��90��-��AON��-��70��-��AON��=20����
���AOM���NOC��������ϵΪ����AOM-��NOC=20����