题目内容
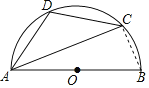
【题目】如图,AB是半圆O的直径,弦AC=4,∠CAB=60°,点D是弧BC上的一个动点,作CG⊥AD,连结BG,在点D移动的过程中,BG的最小值是___________.
【答案】![]() -2
-2
【解析】
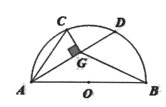
以AC为直径作圆O',连接BO',BC,在点D移动的过程中,点G在以AC为直径的圆上运动,当O'、G、B三点共线时BG的值最小,利用勾股定理求出BO',由BG= BO'-G O'可得结果.
以AC为直径作圆O',连接BO',BC,如下图所示, 
∵CG⊥AD,
∴∠AGC=90°,
∴在点D移动的过程中,点G在以AC为直径的圆上运动,
∵AB是圆O的直径,
∴∠ACB=90°,
在Rt△ABC中,AC=4,∠CAB=60°
∴![]() ,
,
在Rt△BCO'中,CO'=G O'=![]() AC=2,
AC=2,
∴![]()
∵BG+GO'≥BO'
∴当O'、G、B三点共线时BG的值最小,
最小值BG= BO'-G O'=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.