题目内容
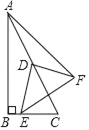
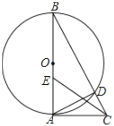
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证:![]() ;
;
(3)在![]() 上取一点
上取一点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)相切,详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)要证明AC与⊙O相切.证得∠BAC=90°即可;
(2)证明△BCA~△ACD,即可得到CA2=CDCB;
(3)设⊙O的半径为![]() ,EC=
,EC=![]() ,AC=r,EB=EC=
,AC=r,EB=EC=![]() ,AE=
,AE=![]() ,在Rt△AEC中,EC2=AE2+AC2,列出方程
,在Rt△AEC中,EC2=AE2+AC2,列出方程![]() 2=(
2=(![]() )2+
)2+![]() 2,求出
2,求出![]() 的值,即可求tan∠ACE的值.
的值,即可求tan∠ACE的值.
(1)相切.理由是:
∵AB是直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵∠DAC=∠B,
∴∠DAC+∠BAD=90°,
∴∠BAC=90°,
∴BA⊥AC,
∴AC是⊙O的切线;
(2)在Rt△BCA和Rt△ACD中,
∠BAC=∠ADC=90°,∠BCA=∠ACD ,
∴△BCA![]() △ACD,
△ACD,
∴![]() ,
,
∴![]() ;
;
(3)设⊙O的半径为r,EC=x,
∵AB=2AC,
∴AC=r,
∵∠BCE=∠B,
∴EB=EC=x,
∴AE=2r﹣x,
在Rt△AEC中,
∵EC2=AE2+AC2,即![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目