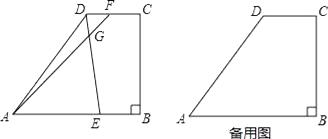
题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是 . 
【答案】4
【解析】解:∵AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点, ∴CG=GD,CF=FG= ![]() CG,
CG,
∵CF=2,∴CG=GD=2×2=4,FD=2+4=6,
由相交弦定理得EFAF=CFFD,
即EF= ![]() =
= ![]() =4,
=4,
故EF的长是4.
【考点精析】解答此题的关键在于理解相交弦定理的相关知识,掌握圆内的两条相交弦,被交点分成的两条线段长的积相等;如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目