题目内容
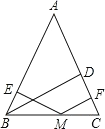
【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
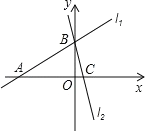
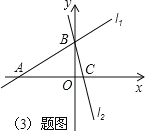
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是![]() ,求点 M 的坐标.
,求点 M 的坐标.
【答案】(1)证明见解析;(2)h1﹣h2=h;(3)点 M 的坐标为 M(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)根据S△ABC=S△ABM+S△AMC即可求出答案;
(2)h1-h2=h;
(3)先求得△ABC为等腰三角形,再根据(1)(2)的结果分①当点M在BC边上时,②当点M在CB延长线上时,求得M的坐标.③当点M在BC的延长线上时,h1=![]() <h,不存在.
<h,不存在.
(1)证明:连接 AM,
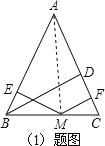
由题意得 h1=ME,h2=MF,h=BD,
∵S△ABC=S△ABM+S△AMC,
S△ABM=![]() ×AB×ME=
×AB×ME=![]() ×AB×h1,
×AB×h1,
S△AMC=![]() ×AC×MF=
×AC×MF=![]() ×AC×h2,
×AC×h2,
又∵S△ABC=![]() ×AC×BD=
×AC×BD=![]() ×AC×h,AB=AC,
×AC×h,AB=AC,
∴![]() ×AC×h=
×AC×h=![]() ×AB×h1+
×AB×h1+![]() ×AC×h2,
×AC×h2,
∴h1+h2=h.
(2)如图所示:
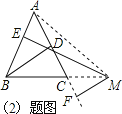
h1﹣h2=h.
(3)解:在 y=![]() x+3 中,令 x=0 得 y=3;令 y=0 得 x=﹣4,所以 A(﹣4,0),B(0,3)
x+3 中,令 x=0 得 y=3;令 y=0 得 x=﹣4,所以 A(﹣4,0),B(0,3)
同理求得 C(1,0).
AB=![]() =5,AC=5,所以 AB=AC,
=5,AC=5,所以 AB=AC,
即△ABC 为等腰三角形.
(ⅰ)当点 M 在 BC 边上时,由 h1+h2=h 得:![]() +My=OB,My=3﹣
+My=OB,My=3﹣![]() =
=![]() , 把它代入y=﹣3x+3 中求得:Mx=
, 把它代入y=﹣3x+3 中求得:Mx=![]() ,所以此时 M(
,所以此时 M(![]() ,
,![]() )
)
(ⅱ)当点 M 在 CB 延长线上时,由 h1﹣h2=h 得:My﹣![]() =OB,My=3+
=OB,My=3+![]() =
=![]() ,
,
把它代入 y=﹣3x+3 中求得:Mx=﹣![]() , 所以此时 M(﹣
, 所以此时 M(﹣![]() ,
,![]() ).
).
综合(ⅰ)、(ⅱ)知:点 M 的坐标为 M(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).

 黄冈创优卷系列答案
黄冈创优卷系列答案