题目内容
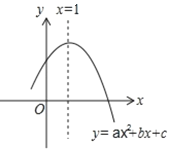
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() .
.

(1)求此抛物线的函数表达式;
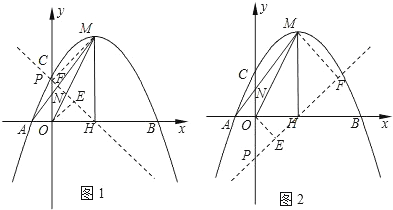
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若 ![]() 时,求点P的坐标;
时,求点P的坐标;
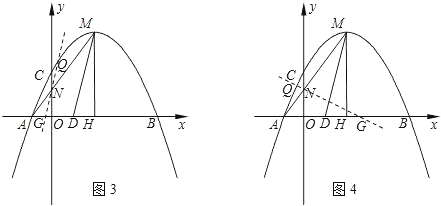
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG 与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由。
【答案】(1) y=-![]() (x-2)2+4.(2) P(0,2),P(0,-2).(3) y=4x+
(x-2)2+4.(2) P(0,2),P(0,-2).(3) y=4x+![]() 或y=-
或y=-![]() .
.
【解析】
试题分析:(1)由抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() ,求出c的值,进而求出抛物线方程;
,求出c的值,进而求出抛物线方程;
(2)如图1,由OE⊥PH,MF⊥PH,MH⊥OH,可证△OEH∽△HFM,可知HE,HF的比例关系,求出P点坐标;
(3)首先求出D点坐标,写出直线MD的表达式,由两直线平行,两三角形相似,可得NG∥MD,直线QG解析式.
试题解析:(1)∵M为抛物线![]() 的顶点,
的顶点,
∴M(2,c).
∴OH=2,MH=|c|.
∵a<0,且抛物线与x轴有交点,
∴c>0,
∴MH=c,
∵sin∠MOH=![]() ,
,
∴![]() .
.
∴OM=![]() c,
c,
∵OM2=OH2+MH2,
∴MH=c=4,
∴M(2,4),
∴抛物线的函数表达式为:y=-![]() (x-2)2+4.
(x-2)2+4.
(2)如图1,∵OE⊥PH,MF⊥PH,MH⊥OH,
∴∠EHO=∠FMH,∠OEH=∠HFM.
∴△OEH∽△HFM,
∴![]() ,
,
∵![]() ,
,
∴MF=HF,
∴∠OHP=∠FHM=45°,
∴OP=OH=2,
∴P(0,2).
如图2,同理可得,P(0,-2).
(3)∵A(-1,0),
∴D(1,0),
∵M(2,4),D(1,0),
∴直线MD解析式:y=4x-4,
∵ON∥MH,∴△AON∽△AHM,
∴![]() ,
,
∴AN=![]() ,ON=
,ON=![]() ,N(0,
,N(0,![]() ).
).
如图3,若△ANG∽△AMD,可得NG∥MD,
∴直线QG解析式:y=4x+![]() ,
,
如图4,若△ANG∽△ADM,可得![]()
∴AG=![]() ,
,
∴G(![]() ,0),
,0),
∴QG:y=-![]() ,
,
综上所述,符合条件的所有直线QG的解析式为:y=4x+![]() 或y=-
或y=-![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案