题目内容
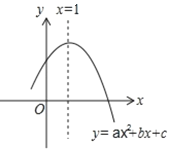
【题目】如图,二次函数![]() 的图象过点A(3,0),对称轴为直线
的图象过点A(3,0),对称轴为直线![]() ,给出以下结论:
,给出以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④若M(-3,
;④若M(-3,![]() )、N(6,
)、N(6,![]() )为函数图象上的两点,则
)为函数图象上的两点,则![]() ,其中正确的是____________.(只要填序号)
,其中正确的是____________.(只要填序号)
【答案】①②③
【解析】
①根据函数图像的开口、对称轴以及与y轴的交点可得出a、b、c的正负,即可判断正误;
②根据函数对称轴可得出a、b之间的等量关系,将![]() 转化为
转化为![]() ,再由函数与x轴的交点关于对称轴对称,可得出另一个交点是(-1,0),即可得出
,再由函数与x轴的交点关于对称轴对称,可得出另一个交点是(-1,0),即可得出![]() 的结果,即可判断正误;
的结果,即可判断正误;
③根据a、b之间的等量关系,将不等式中的b代换成a,化简不等式即可判断正误;
④根据开口向下的函数有最大值,距离顶点越近的函数值越大,先判断M、N距离顶点的距离即可判断两个点y值得大小.
解:①∵函数开口向下,∴![]() ,
,
∵对称轴![]() ,
,![]() ,∴
,∴![]() ;
;
∵函数与y轴交点在y轴上半轴,∴![]() ,
,
∴![]() ;所以①正确;
;所以①正确;
②∵函数对称轴为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵A(3,0)是函数与x轴交点,对称轴为![]() ,
,
∴函数与x轴另一交点为(-1,0);
∵当![]() 时,
时,![]() ,
,
∴![]() ,②正确;
,②正确;
③∵函数对称轴为![]() ,
,
∴![]() ,
,
∴将![]() 带入
带入![]() 可化为:
可化为:![]() ,
,
∵![]() ,不等式左右两边同除a需要不等号变方向,可得:
,不等式左右两边同除a需要不等号变方向,可得:
![]() ,
,
即![]() ,此不等式一定成立,所以③正确;
,此不等式一定成立,所以③正确;
④M(-3,![]() )、N(6,
)、N(6,![]() )为函数图象上的两点,
)为函数图象上的两点,
∵点M距离顶点4个单位长度,N点距离顶点5个单位长度,函数开口向下,距离顶点越近,函数值越大,
∴![]() ,所以④错误.
,所以④错误.
故答案为①②③.

【题目】某商场销售A、B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
教学设备 | A | B |
进价(万元/套) | 3 | 2.4 |
售价(万元/套) | 3.3 | 2.8 |
该商场计划购进两种教学设备若干套,共需132万元,全部销售后可获毛利润18万元.
(1)该商场计划购进A、B两种品牌的教学设备各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍.若用于购进这两种教学设备的总资金不超过138万元,则A种设备购进数量最多减少多少套?