题目内容
【题目】今年6月份，某果农收获荔枝30吨，香蕉13吨，现计划租用甲、乙两种货车共10辆将这批水果全部运往港口，已知一辆甲种货车可装荔枝和香蕉共5吨，且一辆甲种货车可装的荔枝重量（单位：吨）是其可装的香蕉重量的4倍，一辆乙种货车可装荔枝香蕉各2吨；
（1）一辆甲种货车可装载荔枝、香蕉各多少吨？
（2）该果农安排甲、乙两种货车时有几种方案？请你帮助设计出来；
（3）若甲种货车每辆要付运输费2000元，乙种货车每辆要付运输费1300元，则该果农应选择哪种方案？使运费最少？最少运费是多少元？
【答案】（1）一辆甲种货车可装载荔枝4吨，香蕉1吨；（2）共有三种方案，方案1：安排5辆甲种货车，5辆乙种货车；方案2：安排6辆甲种货车，4辆乙种货车；方案3：安排7辆甲种货车，3辆乙种货车．（3）该果农应选方案1，使运费最少，最少运费是16500元．
【解析】
（1）可设一辆甲种货车可装载荔枝x吨，香蕉y吨，根据“一辆车总共装5吨”，有
，根据“可装的荔枝重量是其可装的香蕉重量的4倍”，有
，联立解二元一次方程组即可.
（2）可以设安排m辆甲种货车，安排（10﹣m）辆乙种货车，必须使两种车装载荔枝总量大于等于30吨，则有
，装载香蕉总量大于等于13吨，则有
，联立解一元一次不等式组，注意只取整数.
（3）根据第（2）题得出的方案逐一计算，取最小费用即可.
（1）设一辆甲种货车可装载荔枝x吨，香蕉y吨，
依题意，得：
，
解得：
．
答：一辆甲种货车可装载荔枝4吨，香蕉1吨．
（2）设安排m辆甲种货车，则安排（10﹣m）辆乙种货车，
依题意，得：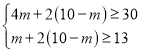
，
解得：5≤m≤7．
∵m为整数，
∴m＝5，6，7，
∴共有三种方案，方案1：安排5辆甲种货车，5辆乙种货车；方案2：安排6辆甲种货车，4辆乙种货车；方案3：安排7辆甲种货车，3辆乙种货车．
（3）方案1所需费用2000×5+1300×5＝16500（元）；
方案2所需费用2000×6+1300×4＝17200（元）；
方案3所需费用2000×7+1300×3＝17900（元）．
∵16500＜17200＜17900，
∴该果农应选方案1，使运费最少，最少运费是16500元．
【题目】某商场销售A、B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：
教学设备 | A | B |
进价（万元/套） | 3 | 2.4 |
售价（万元/套） | 3.3 | 2.8 |
该商场计划购进两种教学设备若干套，共需132万元，全部销售后可获毛利润18万元．
（1）该商场计划购进A、B两种品牌的教学设备各多少套？
（2）通过市场调查，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍．若用于购进这两种教学设备的总资金不超过138万元，则A种设备购进数量最多减少多少套？
