Question

【题目】如图，正方形ABCD中，AB=2，将线段CD绕点C顺时针旋转90°得到线段CE，线段BD绕点B顺时针旋转90°得到线段BF，连接BF，则图中阴影部分的面积是_____．

Answer 1

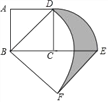
【答案】6﹣π

【解析】过F作FM⊥BE于M，则∠FME=∠FMB=90°，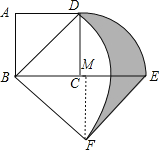

∵四边形ABCD是正方形，AB=2，
∴∠DCB=90°，DC=BC=AB=2，∠DCB=45°，
由勾股定理得：BD=2，
∵将线段CD绕点C顺时针旋转90°得到线段CE，线段BD绕点B顺时针旋转90°得到线段BF，
∴∠DCE=90°，BF=BD=2，∠FBE=90°-45°=45°，
∴BM=FM=2，ME=2，
∴阴影部分的面积=×2×2+×4×2+-=6-π.
故答案为：6-π．