题目内容
【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），该抛物线的对称轴为直线x=﹣1，若点C（﹣ 
，y1），D（﹣ 
，y2），E（ 
，y3）均为函数图象上的点，则y1 ， y2 ， y3的大小关系为 ．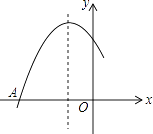 
【答案】y3＜y1＜y2
【解析】解：∵抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣1，开口向下，
∴离对称轴近的点的函数值大，
∵|﹣ 
+1|＜|﹣ 
+1|＜| 
+1|
∴y3＜y1＜y2 ．
所以答案是y3＜y1＜y2 ．
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
练习册系列答案
相关题目
