题目内容
【题目】平面内的两条直线有相交和平行两种位置关系.
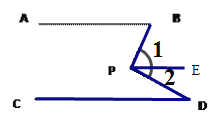
(1)AB∥CD.如图1,点P在AB,CD外部时,由AB∥CD,有∠B=∠BOD.又因为∠BOD是△POD的外角,故∠BOD=∠BPD +∠D ,得∠BPD=∠B-∠D.如图2,将点P移到AB,CD内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
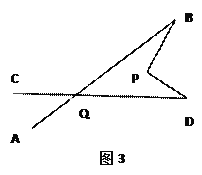
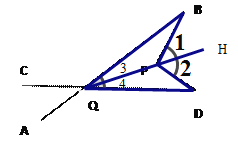
(2)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?说明理由.
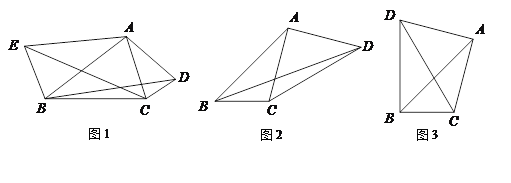
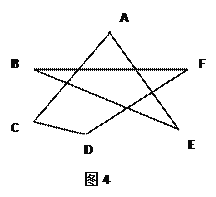
(3)根据(2)的结论,求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.
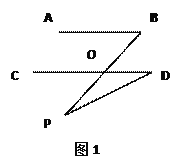
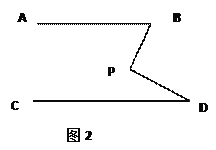
【答案】(1)不成立,∠BPD=∠B+∠D.
(2) ∠BPD=∠B+∠D+∠BQD.
(3) 360°
【解析】【试题分析】(1)利用两直线平行,内错角相等,得:PE//AB,则![]() ;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则
;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则![]() ,利用等量代换得:∠BPD=
,利用等量代换得:∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)利用三角形的外角等于不相邻的两个内角和,得![]() ,再利用角度转化即可.即
,再利用角度转化即可.即![]() =
= ![]() .
.
(3)利用转化的思想,利用外角的性质,将6个角的和转化为四边形的内角和,即360°.
【试题解析】
(1)不成立,∠BPD=∠B+∠D.
理由:如图,作PE//AB,则![]() ,因为AB//CD,所以PE//CD,则
,因为AB//CD,所以PE//CD,则![]() ,所以∠BPD=
,所以∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)作射线QP, ![]() ,则
,则![]() =
= ![]() .
.
即: ![]() =
= ![]() .
.
(3)由题意得: ![]() ,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+
,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+![]() =360°.
=360°.


 阅读快车系列答案
阅读快车系列答案【题目】我市某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元) | … | 70 | 90 | … |
销售量y(件) | … | 3000 | 1000 | … |
(1)求销售量y(件)与售价x(元)之间的函数表达式.
(2)当售价为80元时,工艺品厂每天获得的利润为多少元?