题目内容
【题目】已知二次函数:![]() .
.
(1)求证:二次函数的图象与x轴有两个交点;
(2)当二次函数的图象与x轴的两个交点的横坐标均为整数,且a为负整数时,求a的值及二次函数的解析式并画出二次函数的图象(不用列表,只要求用其与x轴的两个交点A,B(A在B的左侧),与y轴的交点C及其顶点D这四点画出二次函数的大致图象,同时标出A,B,C,D的位置);
(3)在(2)的条件下,二次函数的图象上是否存在一点P使![]() ?如果存在,求出点P的坐标;如果不存在,请说明理由.
?如果存在,求出点P的坐标;如果不存在,请说明理由.

【答案】(1)见解析;(2)![]() ,
,![]() ,函数图象如图所示见解析;(3)存在这样的点P,点P的坐标为
,函数图象如图所示见解析;(3)存在这样的点P,点P的坐标为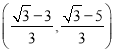 或
或![]() .
.
【解析】
(1)1)将解析式右边因式分解得抛物线与x轴的交点为(2,0)、(![]() ,0),结合a<0即可得证;
,0),结合a<0即可得证;
(2)根据题意求出![]() ,再求出函数与x轴的交点,即可作图;
,再求出函数与x轴的交点,即可作图;
(3)根据题意作出图像,根据题意分两种情况讨论:①当点P在直线AC上方时,记直线PC与x轴的交点为E,根据![]() 求出
求出![]() ,因此
,因此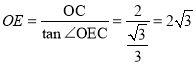 ,求出
,求出![]() ,则可求出求得直线CE解析式为
,则可求出求得直线CE解析式为![]() ,再联立两直线即可求出P点坐标;②当点P在直线AC下方时, 同理求出P的坐标.
,再联立两直线即可求出P点坐标;②当点P在直线AC下方时, 同理求出P的坐标.
(1)∵![]() ,且
,且![]() ,
,
∴抛物线与x轴的交点为![]() 、
、![]() ,
,
则二次函数的图象与x轴有两个交点;
(2)∵两个交点的横坐标均为整数,且a为负整数,
∴![]() ,
,
则抛物线与x轴的交点A的坐标为![]() 、B的坐标为
、B的坐标为![]() ,
,
∴抛物线解析式为![]()
![]()
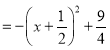 ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
函数图象如图1所示:
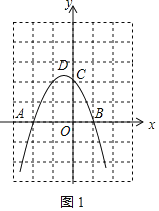
(3)存在这样的点P,
∵![]() ,
,
∴![]() ,
,
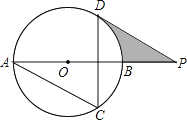
如图2,当点P在直线AC上方时,记直线PC与x轴的交点为E,
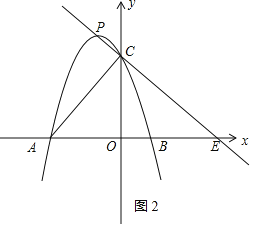
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
∴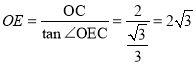 ,
,
则![]() ,
,
求得直线CE解析式为![]() ,
,
联立 ,
,
解得![]() 或
或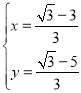 ,
,
∴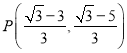 ;
;
如图3,当点P在直线AC下方时,记直线PC与x轴的交点为F,
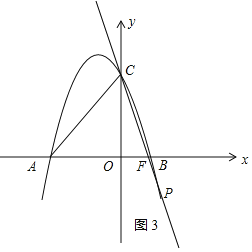
∵![]() ,
,![]() ,
,
∴![]() ,
,
则![]() ,
,
∴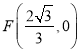 ,
,
求得直线PC解析式为![]() ,
,
联立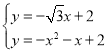 ,
,
解得:![]() 或
或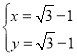 ,
,
∴![]() ,
,
综上,点P的坐标为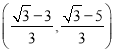 或
或![]() .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目