题目内容
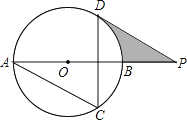
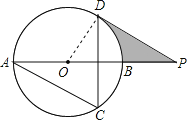
【题目】如图,AB是⊙O的直径,AC,DC是⊙O的两条弦,点P在AB的延长线上.已知,∠ACD=60°,∠APD=30°
(1)求证:PD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
【答案】(1)见解析;(2)2![]() ﹣
﹣![]() π.
π.
【解析】
(1)直接利用已知得出∠ODP=90°,进而得出答案;
(2)直接利用△ODP的面积减去扇形DOB的面积进而得出答案.
(1)证明:连接OD,
∵∠ACD=60°,
∴∠AOD=120°,
∴∠BOD=60°,
∵∠APD=30°,
∴∠ODP=90°,
即PD⊥OD,
∴PD是⊙O的切线;
(2)解:∵在Rt△POD中,OD=2cm,∠APD=30°,
∴PD=2![]() ,
,
∴图中阴影部分的面积=![]() ×2×2
×2×2![]() ﹣
﹣![]() ×π×22
×π×22
=2![]() ﹣
﹣![]() π.
π.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目