Question

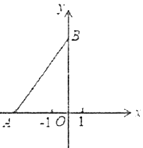
【题目】如图，在平面直角坐标系中，点，为轴负半轴上一点，点为轴正半轴上一点，其中满足方程．

（1）求点、的坐标；

（2）点为轴负半轴上一点，且的面积为，求点的坐标；

（3）在上是否存在一点，使的面积等于的面积的一半，若存在，求出相应的点的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）点A坐标为（-3，0），点B坐标为（0，4）；（2）点C坐标为（0，-4）；（3）存在，点P坐标为（，0）或（-，0）．

【解析】

（1）解方程可求出b的值，即可得A、B坐标；

（2）根据A、B坐标可得OA、OB的长，利用三角形面积公式可求出BC的长，根据点C在y轴负半轴可得OC的长，可得C点坐标；

（3）利用三角形面积公式可求出OP的长，分点P在原点左边和右边两种情况，求出OP的坐标即可．

（1）∵，

∴b=1，

∵，，

∴点A坐标为（-3，0），点B坐标为（0，4）．

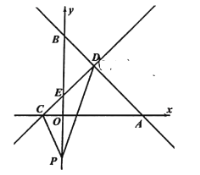
（2）如图，∵A（-3，0），B（0，4），

∴OA=3，OB=4，

∵△ABC的面积为12，

∴BC·OA=12，即×3×BC=12，

解得：BC=8，

∵点为轴负半轴上一点，

∴OC=BC-OB=8-4=4，

∴点C坐标为（0，-4）．

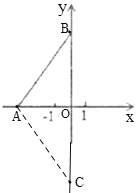
（3）如图，∵的面积等于的面积的一半，△ABC的面积为12，

∴△PBC的面积为6，

∴BC·OP=6，即×8×OP=6，

解得：OP=，

当点P在原点左边时，点P坐标为（-，0），

当点P在原点右边时，点P坐标为（，0），

∴存在一点，使的面积等于的面积的一半，点P坐标为（，0）或（-，0）．