题目内容
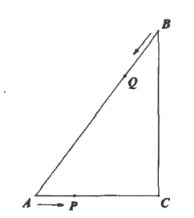
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交于y轴于点H.
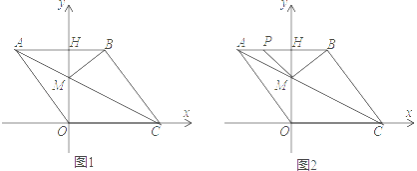
(1)连接BM,动点P从点A出发,沿折线ABC方向以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形BMP?如存在,求出t的值;如不存在,请说明理由.
【答案】(1)详见解析;(2)当t=1或![]() 时,△PMB为以BM为腰的等腰三角形.
时,△PMB为以BM为腰的等腰三角形.
【解析】
(1)设点M到BC的距离为h,由△ABC的面积易得h,利用分类讨论的思想,三角形的面积公式①当P在直线AB上运动;②当P运动到直线BC上时分别得△PBM的面积;
(2)分类讨论:①当MB=MP时,PH=BH,解得t;②当BM=BP时,利用勾股定理可得BM的长,易得t.
解:
(1)设点M到BC的距离为h,
由S△ABC=S△ABM+S△BCM,
即![]() ,
,
∴h=![]() ,
,
①当P在直线AB上运动时△PBM的面积为S与P的运动时间为t秒关系为:
S=![]() (5﹣t)×
(5﹣t)×![]() ,即S=﹣
,即S=﹣![]() (0≤t<5);
(0≤t<5);
②当P运动到直线BC上时△PMB的面积为S与P的运动时间为t秒关系为:
S=![]() [5﹣(10﹣t)]×
[5﹣(10﹣t)]×![]() ,即S=
,即S=![]() t-
t-![]() (5<t≤10);
(5<t≤10);
(2)存在①当MB=MP时,
∵点A的坐标为(﹣3,4),AB=5,MB=MP,MH⊥AB,
∴PH=BH,即3﹣t=2,
∴t=1;
②当BM=BP时,即5﹣t=![]() ,
,
∴ ![]()
综上所述,当t=1或![]() 时,△PMB为以BM为腰的等腰三角形.
时,△PMB为以BM为腰的等腰三角形.

练习册系列答案
相关题目