题目内容
【题目】如图,在平面直角坐标系中,边长为4的等边![]() 的边
的边![]() 在
在![]() 轴的负半轴上,反比例函数
轴的负半轴上,反比例函数![]() 的图象经过
的图象经过![]() 边的中点
边的中点![]() ,且与
,且与![]() 边交于点
边交于点![]() .
.
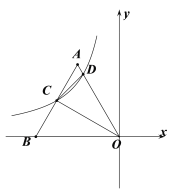
(1)求![]() 的值;
的值;
(2)连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(3)若直线![]() 与直线
与直线![]() 平行,且与
平行,且与![]() 的边有交点,直接写出
的边有交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 3;(3)
3;(3)![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,根据等边三角形的性质可求出点C的坐标,把点C的坐标代入反比例函数
,根据等边三角形的性质可求出点C的坐标,把点C的坐标代入反比例函数![]() 即可求出k的值;
即可求出k的值;
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .再根据等边三角形的性质可求得AF,BF,从而求出点A的坐标.再用待定系数法求出直线OA的解析式,让反比例函数解析 式与直线OA的解析式联立解方程组求出点D的坐标,三角形OCD的面积=四边形ODCE的面积-三角形OCE的面积.从而得到求解.
.再根据等边三角形的性质可求得AF,BF,从而求出点A的坐标.再用待定系数法求出直线OA的解析式,让反比例函数解析 式与直线OA的解析式联立解方程组求出点D的坐标,三角形OCD的面积=四边形ODCE的面积-三角形OCE的面积.从而得到求解.
(3)由图形可知当![]() 过点C时n有最大值,当
过点C时n有最大值,当![]() 时n有最小值.
时n有最小值.
(1)如图1,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]() 是
是![]() 中点,
中点,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
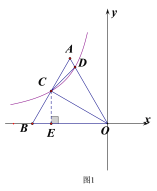
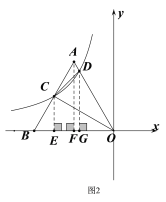
(2)如图2.过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
则![]() ,
,![]() ,
,
∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)可知反比例函数解析式为![]() ,
,
联立方程组: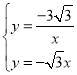 ,
,
解得: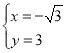 或
或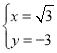 (舍),
(舍),
∴![]() ,
,
∴![]()
![]()
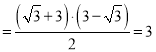 .
.
(3)![]() .理由如下:
.理由如下:
∵![]() ,
,![]() ,
,
∴![]() =1.
=1.
∵直线![]() 与直线
与直线![]() 平行,
平行,
∴m=1.
∴直线![]() 解析式为
解析式为![]() .
.
∴把![]() 代入
代入![]() ,得:
,得:
n=![]() .
.
把![]() 代入
代入![]() ,得:
,得:
n=0.
∴![]()

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.