题目内容
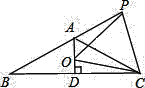
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线一点,点
延长线一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .
.
(1)已知![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() 是等边三角形;
是等边三角形;
(3)求证:![]() .
.
【答案】(1)12°;(2)证明见详解;(3)证明见详解.
【解析】
(1)连接OB,根据等腰三角形的性质可得OB=OC,再利用等边对等角可得∠APO=∠ABO,∠OBD=∠OCD,则∠APO+∠OCD=∠ABO+∠OBD=∠ABD,据此即可求解;
(2)证明∠POC =60°且OP=OC,即可证明![]() 是等边三角形;
是等边三角形;
(3)先证明∠APO=∠CPE,利用SAS即可证明![]() ,则AO=CE,即AC=AE+CE=AO+AP.
,则AO=CE,即AC=AE+CE=AO+AP.
(1)如图所示,连接OB,
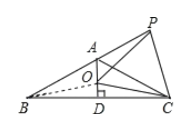
∵![]() ,
,![]() ,
,![]() ,
,
∴BD=CD,∠BAD=![]() ∠BAC=60°,
∠BAC=60°,
∴OB=OC,∠ABC=30°,
∵OP=OC,
∴OP=OC=OB,
∴∠APO=∠ABO,∠OBD=∠OCD,
∴∠APO+∠OCD=∠ABO+∠OBD=∠ABD,
∵∠ABD=30°,∠APO=18°,
∴∠DCO=∠ABD-∠APO=30°-18°=12°;
(2)∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-∠OPC-∠OCP=60°,
∵OP=OC,
∴![]() 是等边三角形;
是等边三角形;
(3)如图所示,在AC上截取AE=PA,连接PE,
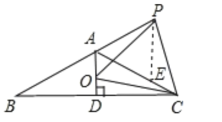
∵∠PAE=180°-∠BAC=60°,
∴![]() 是等边三角形,
是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
又∵OP=CP,PA=PE,
∴![]() (SAS),
(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个) | 售价(元/个) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?