题目内容
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
![]()
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16 cm,水面最深地方的高度为4 cm,求这个圆形截面的半径;
(3)在(2)的条件下,小明把一只宽12 cm的方形小木船放在修好后的圆柱形水管里,已知船高出水面13 cm,问此小船能顺利通过这个管道吗?
【答案】(1)补图见解析;(2)这个圆形截面的半径为10 cm;(3)小船能顺利通过这个管道.
【解析】
(1)在弧AB上任取一点C,连接AC,作弦AC的垂直平分线,两线交点作为圆心O,OA作为半径,画圆即为所求图形.
(2)过O作OE⊥AB于D,交弧AB于E,连接OB,根据垂径定理得到BD=![]() AB=
AB=![]() ×16=8 cm,然后根据勾股定理列出关于圆形截面半径的方程求解.
×16=8 cm,然后根据勾股定理列出关于圆形截面半径的方程求解.
(3)连接OM,设MF=6 cm,可求得此时OF的高,即可求得DF的长,比较13 cm,即可得到此时小船能顺利通过这个管道.
(1)在弧AB上任取一点C,连接AC,作弦AC,BC的垂直平分线,两线交点作为圆心O,OA作为半径,画圆即为所求图形.
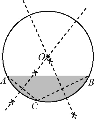

(2)过点O作OE⊥AB交AB于点D,交弧AB于点E,连接OB.
∵OE⊥AB,∴BD=![]() AB=
AB=![]() ×16=8 cm,
×16=8 cm,
由题意可知,ED=4 cm,设半径为x cm,则OD=(x-4) cm.
在Rt△BOD中,由勾股定理得OD2+BD2=OB2.
∴(x-4)2+82=x2,解得x=10,即这个圆形截面的半径为10 cm.
(3)如图,小船能顺利通过这个管道.理由:连接OM,设MF=6 cm,
∵EF⊥MN,OM=10 cm,
在Rt△MOF中,OF=![]() =8 cm,∵DF=OF+OD=8+6=14 cm,
=8 cm,∵DF=OF+OD=8+6=14 cm,
∵14 cm>13 cm,∴小船能顺利通过这个管道.

【题目】2017年6月22日至7月2日,11天湖南地区持续降大到暴雨,总量达570亿立方米的雨水从天而降,倾泻到三湘大地,全省14个市州120个县(市、区)1621个多镇受灾,现有三批救灾物资从长沙岀发送往某受灾乡镇,前两批物资运货情况如图所示:
火车皮(单位:节) | 汽车(单位:辆) | 物质重量(单位:吨) | |
第一批 | 4 | 16 | 264 |
第二批 | 6 | 10 | 340 |
(1)每节火车皮和每辆汽车平均各能装多少吨物资?
(2)已知火车皮的装运费为30元吨,汽车的装运费为100元/吨.若第三批救灾物资需要5节火车皮和15辆汽车正好装完,共需要装运费多少元?