题目内容
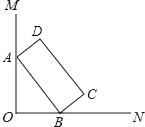
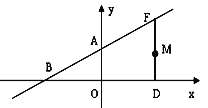
【题目】如图,一次函数![]() 的图象交y轴于点A,交x轴于点B,点F在射线BA上,过点F作x轴的垂线,点D为垂足,
的图象交y轴于点A,交x轴于点B,点F在射线BA上,过点F作x轴的垂线,点D为垂足,
⑴若OD=6,求F点的坐标;
(2)若OD=12,M在线段FD上,M的纵坐标为m,连接BM,用含有m的代数式表示△BMF的面积.
【答案】(1)![]() ;(2)150-10m
;(2)150-10m
【解析】
(1)分点D在x轴正半轴和负半轴两种情况讨论即可;
(2)先求得B的坐标,即可得到BD的长,再令x=12,求得点F的坐标,即可得到FM的长,再利用三角形面积公式即可表示出△BMF的面积.
(1)∵OD=6,
∴点D横坐标为6或-6,
∴当x=6时,把x=6代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ;
;
当x=-6时,把x=-6代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ;
;
故点![]() ;
;
(2)令y=0,得![]() =0,解得x=-8,
=0,解得x=-8,
∴B(-8,0),
把x=12代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ,
,
∴FM=15-m,BD=8+12=20,
∴S△BMF=![]() FM·BD=
FM·BD=![]() ×(15-m) ×20=150-10m;
×(15-m) ×20=150-10m;

练习册系列答案
相关题目