题目内容
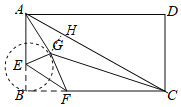
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

【答案】![]() .
.
【解析】
先确定出EG⊥AC时,四边形AGCD的面积最小,再用锐角三角函数求出点G到AC的距离,最后用面积之和即可得出结论.
解:∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得,AC=5,
∵AB=3,AE=2,
∴点F在BC上的任何位置时,点G始终在AC的下方,
设点G到AC的距离为h,
∵S四边形AGCD=S△ACD+S△ACG=![]() AD×CD+
AD×CD+![]() AC×h=
AC×h=![]() ×4×3+
×4×3+![]() ×5×h=
×5×h=![]() h+6,
h+6,
∴要四边形AGCD的面积最小,即h最小,
∵点G是以点E为圆心,BE=1为半径的圆上在矩形ABCD内部的一部分点,
∴EG⊥AC时,h最小,即点E,点G,点H共线.
由折叠知∠EGF=∠ABC=90°,
延长EG交AC于H,则EH⊥AC,
在Rt△ABC中,sin∠BAC=![]() ,
,
在Rt△AEH中,AE=2,sin∠BAC=![]() =
=![]() ,
,
∴EH=![]() ,AE=
,AE=![]() ,
,
∴h=EH﹣EG=![]() ﹣1=
﹣1=![]() ,
,
∴S四边形AGCD最小=![]() h+6=
h+6=![]() +6=
+6=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目