��Ŀ����
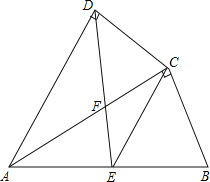
����Ŀ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������ǡ�DOC����������DOC����ʱ�뷽����ת�õ���D��OC����0������ת�ǣ�90��������AC����BD����AC����BD���ཻ�ڵ�M��
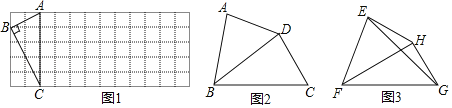
��1�����ı���ABCD�Ǿ���ʱ����ͼ1�������AC����BD����������ϵ�Լ���AMB�����Ĵ�С��ϵ����֤����IJ��룻
��2�����ı���ABCD��ƽ���ı���ʱ����ͼ2����֪AC��kBD��������ʱAC����BD����������ϵ�Լ���AMB�����Ĵ�С��ϵ����֤����IJ��룻
��3�����ı���ABCD�ǵ�������ʱ����ͼ3��AD��BC����ʱ��1��AC����BD����������ϵ�Ƿ��������AMB�����Ĵ�С��ϵ�Ƿ����������֤����ֱ��д�����ۣ�
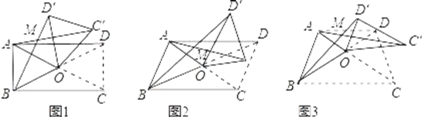
���𰸡���1��BD����AC������AMB����������������2��AC����kBD������AMB����������������3��AC����BD����������AMB����������
��������
��1��ͨ��֤����BOD���ա�AOC���õ�BD����AC������OBD������OAC���������������ڽǺͶ��������AMB����AOB����COD������
��2�����ݣ�1����˼·֤����BOD���ס�AOC�����õ�AC����kBD������BD����OA�ཻ�ڵ�N��������֤�á�BNO����ANM���ٸ����������ڽǺ������AMB������
��3�������õ������ε�����OA=OD,OB=OC,��������ת֤��![]() ,�ɴ�֤����
,�ɴ�֤����![]() �ա�
�ա�![]() ���õ�BD����AC������Ӧ�ǵĵ�����ϵ���ɴ�֤�á�AMB������������
���õ�BD����AC������Ӧ�ǵĵ�����ϵ���ɴ�֤�á�AMB������������
�⣺��1��AC����BD������AMB������
֤�����ھ���ABCD�У�AC��BD��OA��OC��![]() AC��OB��OD��
AC��OB��OD��![]() BD��
BD��
��OA��OC��OB��OD��
�֡�OD��OD����OC��OC����
��OB��OD����OA��OC����
�ߡ�D��OD����C��OC��
��180������D��OD��180������C��OC��
���BOD������AOC����
���BOD���ա�AOC����
��BD����AC����
���OBD������OAC����
��BD����OA�ཻ�ڵ�N��
���BNO����ANM��
��180������OAC������ANM��180������OBD������BNO��
����AMB����AOB����COD������
����������BD����AC������AMB������
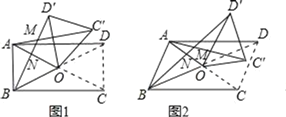
��2��AC����kBD������AMB������
֤��������ƽ���ı���ABCD�У�OB��OD��OA��OC��
�֡�OD��OD����OC��OC����
��OC����OA��OD����OB��
�ߡ�D��OD����C��OC��
��180������D��OD��180������C��OC��
���BOD������AOC����
���BOD���ס�AOC����
��BD����AC����OB��OA��BD��AC��
��AC��kBD��
��AC����kBD����
�ߡ�BOD���ס�AOC����
��BD����OA�ཻ�ڵ�N��
���BNO����ANM��
��180������OAC������ANM��180������OBD������BNO������AMB����AOB������
����������AC����kBD������AMB������
��3�����ڵ�������ABCD�У�OA=OD,OB=OC,
����ת�ã� ![]() ,
,
��![]() ,
,
��![]() ,
,
���![]() �ա�
�ա�![]() ,
,
��AC����BD��, ![]() ,
,
��BD����OA�ཻ�ڵ�N��
�ߡ�ANB=![]() +��AMB=
+��AMB=![]() ,
,![]() ,
,
��![]() ,
,
��AC����BD����������AMB������������