题目内容
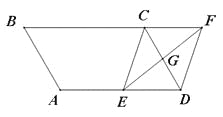
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

【答案】(1)证明见解析;
(2)猜想![]() =
=![]() 或(
或(![]() 理由见解析
理由见解析
【解析】试题分析:
(1)由已知条件易证∠BAE=∠CAD,∠AEB=∠ADC,从而可得△AEB∽△ADC,由此可得![]() ,这样就可得到BE·AD=DC·AE;
,这样就可得到BE·AD=DC·AE;
(2)由(1)中所得△AEB∽△ADC可得![]() =
=![]() ,结合∠DAE=∠BAC可得△BAC∽△EAD,从而可得:
,结合∠DAE=∠BAC可得△BAC∽△EAD,从而可得: ![]() =
=![]() 或(
或(![]() ).
).
试题解析:
①∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠DAC=∠BAE,
∵∠AEB=∠ADB+∠DAE,
∠ADC=∠ADB+∠BDC,
又∵∠DAE=∠BDC,
∴∠AEB=∠ADC,
∴△BEA∽△CDA,
∴![]() =
=![]() ,
,
即BE·AD=CD·AE;
②猜想![]() =
=![]() 或(
或(![]() ),
),
由△BEA∽△CDA可知, ![]() =
=![]() ,即
,即![]() =
=![]() ,
,
又∵∠DAE=∠BAC,
∴△BAC∽△EAD,
∴![]() =
=![]() 或(
或(![]() ).
).

练习册系列答案
相关题目