题目内容
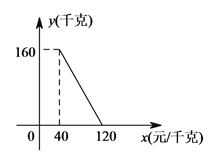
【题目】小阳在如图所示的扇形舞台上沿O-M-N匀速行走，他从点O出发，沿箭头所示的方向经过点M再走到点N，共用时70秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为t（单位：秒），他与摄像机的距离为y（单位：米），表示y与t的函数关系的图象大致如图②，则这个固定位置可能是图①中的
A．点Q B．点P C．点M D．点N
【答案】B
【解析】
试题分析：观察图②中函数图象可知：在小阳从点O出发，沿箭头所示的方向到达点M时， y随t的增大而减小，且并未减小到0，所以摄像机的位置不可能在点Q和M处，所以A、C错误；又小阳从点M到达点N的过程中y随t的增大先减小后增大，所以摄像机的位置不可能在点N处，所以D错误，故B正确，所以选B．
【题目】已知函数y
，请根据已学知识探究该函数的图象和性质．
（1）列表，写出表中a、b，c的值：a= ，b= ，c= ；
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0.5 | a | 2.5 | b | 2.5 | 1 | c | … |
（2）描点，连线：在如图的平面直角坐标系中画出该函数的图象，并写出该函数的一条性质： ；
（3）已知函数y=x﹣1的图象如图所示，结合你所画的函数图象，直接写出不等式
x﹣1的解集： ．
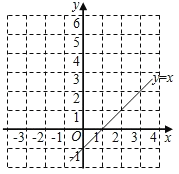
【题目】黔东南州某超市购进甲、乙两种商品，已知购进3件甲商品和2件乙商品，需60元；购进2件甲商品和3件乙商品，需65元．
（1）甲、乙两种商品的进货单价分别是多少？
（2）设甲商品的销售单价为x（单位：元/件），在销售过程中发现：当11≤x≤19时，甲商品的日销售量y（单位：件）与销售单价x之间存在一次函数关系，x、y之间的部分数值对应关系如表：
销售单价x（元/件） | 11 | 19 |
日销售量y（件） | 18 | 2 |
请写出当11≤x≤19时，y与x之间的函数关系式．
（3）在（2）的条件下，设甲商品的日销售利润为w元，当甲商品的销售单价x（元/件）定为多少时，日销售利润最大？最大利润是多少？