题目内容
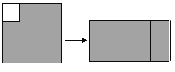
【题目】如图，在边长为a的正方形中挖掉一个边长为b（b＜a）的小正方形，把余下的部分剪拼成一个长方形．通过计算阴影部分的面积，验证了一个等式，这个等式是（ ）
A. a2－b2=（a＋b）（a－b） B. （a＋b）2=a2＋2ab＋b2
C. （a－b）2=a2－2ab＋b2 D. a2－ab=a（a－b）
【答案】A
【解析】
这个图形变换可以用来证明平方差公式：已知在左图中，大正方形减小正方形剩下的部分面积为a2-b2；因为拼成的长方形的长为（a+b），宽为（a-b），根据“长方形的面积=长×宽”代入为：（a+b）×（a-b），因为面积相等，进而得出结论．
由图可知，大正方形减小正方形剩下的部分面积为a2-b2；
拼成的长方形的面积：（a+b）×（a-b），
所以得出：a2-b2=（a+b）（a-b），
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
