题目内容
如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F。
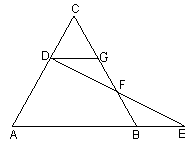
(1)求证:DF=EF;
(2)若△ABC的边长为a,BE的长为b,且a、b满足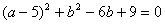 ,求BF的长;
,求BF的长;
(3)若△ABC的边长为5,设CD=x,BF=y,求y与x间的函数关系式,并写出自变量x的取值范围。
(2)若△ABC的边长为a,BE的长为b,且a、b满足
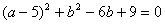 ,求BF的长;
,求BF的长;(3)若△ABC的边长为5,设CD=x,BF=y,求y与x间的函数关系式,并写出自变量x的取值范围。
(1)证明:∵ △ABC是等边三角形
∴∠A=∠B=60°
又 ∵ DG∥AB
∴∠CDG=∠A=60°,∠CGD=∠B=60°
且∠GDF=∠E
∴△CDG是等边三角形
∴ DG=CD=BE
在△DGF和△EBF中
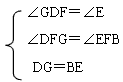
∴△DGF≌△EBF(AAS)
∴DF=EF
(2)解:由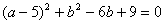 ,得(a-5)2+(b-3)2=0
,得(a-5)2+(b-3)2=0
∵(a-5)2 ≥ 0 ,(b-3)2 ≥ 0
∴(a-5)2=0 ,(b-3)2=0
∴ a=5,b=3 ,即:BC=5,CG=BE=3
又∵ △DGF≌△EBF,∴ BF=GF
∴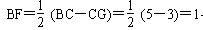
(3)解:∵ CD=x,BF=y ,BC=5
又∵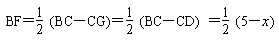
∴所求的解析式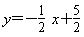
自变量x的取值范围是0<x<5。
∴∠A=∠B=60°
又 ∵ DG∥AB
∴∠CDG=∠A=60°,∠CGD=∠B=60°
且∠GDF=∠E
∴△CDG是等边三角形
∴ DG=CD=BE
在△DGF和△EBF中
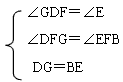
∴△DGF≌△EBF(AAS)
∴DF=EF
(2)解:由
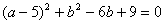 ,得(a-5)2+(b-3)2=0
,得(a-5)2+(b-3)2=0 ∵(a-5)2 ≥ 0 ,(b-3)2 ≥ 0
∴(a-5)2=0 ,(b-3)2=0
∴ a=5,b=3 ,即:BC=5,CG=BE=3
又∵ △DGF≌△EBF,∴ BF=GF
∴
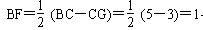
(3)解:∵ CD=x,BF=y ,BC=5
又∵
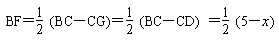
∴所求的解析式
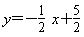
自变量x的取值范围是0<x<5。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.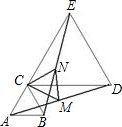 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.