Question

【题目】设a、b、c为实数，且a≠0，抛物线y＝ax2+bx+c，顶点在y＝﹣2上，与x轴交于点A，B，与y轴交于点C，当△ABC为直角三角形时，S△ABC的最大值是（　　）

A.1B.C.3D.4

Answer 1

【答案】D

【解析】

设y＝ax2+bx+c交y轴于点C（0，c），c≠0，交x轴于点A（x1，0）、B（x2，0），且x1＜0＜x2，利用直角三角形被斜边上的高分成的两个三角形与原三角形相似的性质，根与系数的关系，顶点的纵坐标公式，得到：由，可得答案．

解：设y＝ax2+bx+c交y轴于点C（0，c），c≠0，

交x轴于点A（x1，0）、B（x2，0），且x1＜0＜x2，

由△ABC是直角三角形知，

点C必为直角顶点，且c2＝，

由根与系数的关系得，

∴

又即8a＝4+b2≥4，

∴

∴

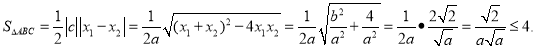
当且仅当时等号成立，因此，Rt△ABC的最大面积是4．

故选：D．