题目内容
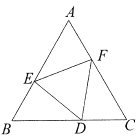
【题目】如图，点D，E，F分别在正三角形
的三边上，且
也是正三角形.若
的边长为a，的边长为b，则
的内切圆半径为（ ）
A.
B.
C.
D.
【答案】B
【解析】
证明△AEF≌△CFD≌△BDE，再求出AH=
（a-b），最后解直角三角形HAM，求出MH的长即可解决问题．
如图，由于△ABC，△DEF都为正三角形，
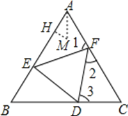
∴AB=BC=CA，EF=FD=DE，∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°，
∴∠1+∠2=∠2+∠3=120°，∠1=∠3；
在△AEF和△CFD中，
，
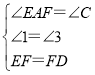∴△AEF≌△CFD（AAS）；
同理可证：△AEF≌△CFD≌△BDE；
∴BE=AF，即AE+AF=AE+BE=a．
设M是△AEF的内心，MH⊥AE于H，
则AH=（AE+AF-EF）=（a-b）；
∵MA平分∠BAC，
∴∠HAM=30°；
∴HM=AHtan30°=（a-b）
=
（a-b）=
．
故选：B．
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤，樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤
.
（1）若小王批发这两种水果正好花费了4400元，那么小王分别购买了多少斤樱桃和榴莲？填写下表，并列方程求解；
品种 | 批发价（元） | 购买斤数 | 小王应付的钱数（元） |
樱桃 | 32 | x | |
榴莲 | 40 |
（2）设小王购买两种水果的总花费为y元，试写出y与x之间的函数表达式.
（3）若要求所批发的榴莲的斤数不少于樱桃斤数的2倍，那么购买樱桃的数量为多少时，可使小王的总花费最少？这个最少花费是多少？
【题目】某剧院举行专场音乐会，成人票每张20元，学生票每张5元．暑假期间，为了丰富广大师生的业余文化生活，影剧院制定了两种优惠方案，方案一：购买一张成人票赠送一张学生票；方案二：按总价的90%付款．某校有4名老师带队，与若干名（不少于4人）学生一起听音乐会．设学生人数为x人，
（x为整数）．
（Ⅰ）根据题意填表：
学生人数/人 | 4 | 10 | 20 | … |
方案一付款金额/元 | 80 | 110 | … | |
方案二付款金额/元 | 90 | 117 | … |
（Ⅱ）设方案一付款总金额为
元，方案二付款总金额为
元，分别求，关于x的函数解析式；
（Ⅲ）根据题意填空：
①若用两种方案购买音乐会的花费相同，则听音乐会的学生有________________人；
②若有60名学生听音乐会，则用方案_______________购买音乐会票的花费少；
③若用一种方案购买音乐会票共花费了450元，则用方案________________购买音乐会票，使听音乐的学生人数多．
