题目内容
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,![]() 是
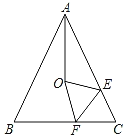
是![]() 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
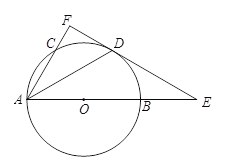
(1)求证:AF⊥EF; (2)若![]() ,AB=5,求线段BE的长.
,AB=5,求线段BE的长.
【答案】(1)见解析;(2)![]()
【解析】
试题(1)连接OD根据切线得出OD⊥EF,根据OA=OD得出∠1=∠3,根据弧的中点得出∠1=∠2,则∠2=∠3,说明OD∥AF,得到切线;(2)连接BD,根据tan∠CAD的值得出tan∠1的值,根据Rt△ADB得出BD和AD的长度,根据平行得出△EDO与△EFA相似,设BE=x,根据相似比得出x的值.
试题解析:(1)证明:连结OD.
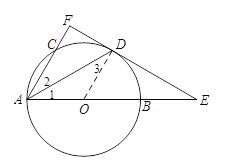
∵直线EF与⊙O相切于点D, ∴OD⊥EF.
∵OA = OD,∴∠1=∠3.∵点![]() 为
为![]() 的中点, ∴∠1=∠2,∴∠2=∠3,∴OD∥AF,∴AF⊥EF.
的中点, ∴∠1=∠2,∴∠2=∠3,∴OD∥AF,∴AF⊥EF.
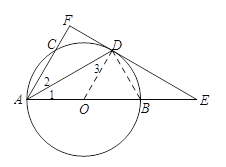
(2)解:连结BD.∵![]() , ∴
, ∴![]() 在Rt△ADB中,AB=5,∴BD=
在Rt△ADB中,AB=5,∴BD=![]() ,AD=
,AD=![]() ,
,
在Rt△AFD中,可得DF=2,AF=4,∵OD∥AF,∴△EDO∽△EFA,∴![]() ,又∵OD=2.5,设BE=x,
,又∵OD=2.5,设BE=x,
∴![]() ,∴
,∴![]() ,即BE=
,即BE=![]() .
.

【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
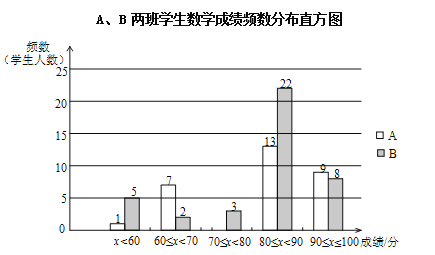
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).