��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��1����2����B��2����1����C��4����3����
��1��������ABC����x��ԳƵġ�A1B1C1��
��2���Ե�OΪλ�����ģ��������л�����A1B1C1��λ��ͼ�Ρ�A2B2C2��ʹ��A2B2C2���A1B1C1�����Ʊ�Ϊ2:1��
��3�����P��a��b��Ϊ��ABC��һ�㣬�����������α任���P�ڡ�A2B2C2�ڵĶ�Ӧ��P2���������� ��
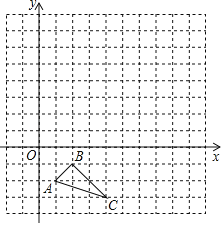
���𰸡���1������������2������������3����2a��-2b����
��������
��1�����ù���x��ԳƵĵ����������������A1��B1��C1��Ȼ��˳�����Ӽ��ɣ�
��2�����ù���ԭ��Ϊλ�����ĵĶ�Ӧ�������֮��Ĺ�ϵ���ѵ�A1��B1��C1�ĺ������궼����2�õ���A2��B2��C2�����꣬Ȼ����㡢˳�����Ӽ��ɣ�
��3�����ã�1����2���е�����任������⣮
�⣺��1����ͼ����A1B1C1��Ϊ����

��2����ͼ����A2B2C2��Ϊ����
��3����P��a��b������һ�α任��Ķ�Ӧ�������Ϊ��a��-b����
��P�������α任���Ķ�Ӧ��P2�������ǣ�2a��-2b����
�ʴ�Ϊ����2a��-2b����

��ϰ��ϵ�д�
�����Ŀ