题目内容
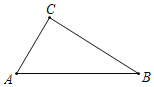
【题目】探究:如图①,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .若
.若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
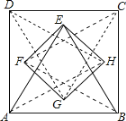
应用:如图②,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() .若
.若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________.
的面积为________.

【答案】![]()
【解析】
探究:过点A作AF⊥CB,交CB的延长线于点F,先判定四边形AFCE为矩形,根据矩形的四个角都是直角可得∠FAE=90°,然后利用同角的余角相等求出∠FAB=∠EAD,再利用“角角边”证明△AFB和△AED全等,根据全等三角形对应边相等可得AE=AF,从而得到四边形AFCE是正方形,然后根据正方形的面积公式列计算即可得解;
应用:过点A作AF⊥CD交CD的延长线于F,连接AC,根据同角的补角相等可得∠ABC=∠ADF,然后利用“角角边”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AF=AE,再根据S四边形ABCD=S△ABC+S△ACD列式计算即可得解.
解:探究:如图①,过点A作AF⊥CB,交CB的延长线于点F,
∵AE⊥CD,∠BCD=90°,
∴四边形AFCE为矩形,
∴∠FAE=90°,
∴∠FAB+∠BAE=90°,
∵∠EAD+∠BAE=90°,
∴∠FAB=∠EAD,
∵在△AFB和△AED中,
 ,
,

∴△AFB≌△AED(AAS),
∴AF=AE,
∴四边形AFCE为正方形,
∴S四边形ABCD=S正方形AFCE=AE2=102=100;
应用:如图,过点A作AF⊥CD交CD的延长线于F,连接AC,
则∠ADF+∠ADC=180°,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADF,
∵在△ABE和△ADF中,
 ,
,
∴△ABE≌△ADF(AAS),
∴AF=AE=19,
∴S四边形ABCD=S△ABC+S△ACD
=![]() BCAE+
BCAE+![]() CDAF
CDAF
=![]() ×10×19+
×10×19+![]() ×6×19
×6×19
=95+57
=152.
故答案为:152.

练习册系列答案
相关题目