题目内容
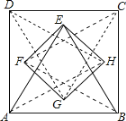
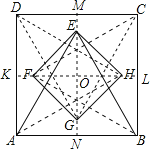
【题目】如图，分别以正方形
的四条边为边，向其内部作等边三角形，得到
、
、
、
，连接
、
、
、
，若
，则四边形
的面积为________．
【答案】
【解析】
先根据题意得出△ABE≌△BCF≌△CDG≌△DAH，连接EG并延长交CD于点M，交AB于点N，连接FH并延长交AD于点k，角BC于点l，
解：∵△ABE、△BCF、△CDG、△DAH均是以2为边长的等边三角形，
∴△ABE≌△BCF≌△CDG≌△DAH．
∵四边形ABCD是正方形，DG=CG，AE=BE，
∴点E线段AB的垂直平分线上，点G在CD的垂直平分线上，AB∥CD，
∴直线MN是线段CD与AB的垂直平分线．
∵AB=CD=2，
∴EN=
，
∴ME=2-，
同理可得GN=2-，
∴EG=2-（2--2-）=2-2．
同理可得，FH=2-2．
∵M、L、N、K分别是四边的中点，
∴EG⊥FH，且OG=OH，
∴四边形EFGH是正方形，
∴OG=OH=
EG=-1，
∴S四边形EFGH=GH2=OG2+OH2=（-1）2+（-1）2=8-4．
故答案为：8-4．
练习册系列答案
阅读快车系列答案
相关题目
