题目内容
【题目】尺规作图与说理(要求保留作图痕迹,不写作法.)如图,在Rt△ABC中,∠ACB=90°
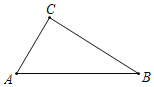
(1)过点C作AB的垂线CD,交AB于点D;
(2)作∠ABC的平分线BE交AC于点E,交CD于点F;
(3)观察线段CE与CF有何数量关系?并说明理由.
【答案】(1)见解析;(2)见解析;(3) CE=CF,理由见解析
【解析】
(1)以C为圆心,以一定长度为半径,使弧与AB交于两点,再作这两点之间线段的中垂线即可;
(2)根据角平分线的画法,用尺规作图即可;
(3)根据等角的余角相等即可证出∠BFD=∠CEB,再根据对顶角相等可得:∠BFD=∠CFE,从而得出:∠CFE=∠CEF,最后根据等角对等边即可证出:CE=CF.
(1)以C为圆心,以一定长度为半径,使弧与边AB交于两点,再作这两点之间线段的中垂线,如图所示,CD即为所求;

(2)以B为圆心,以任意长度为半径,作弧,分别交BA、BC于两点,再分别以这两点为圆心,以大于![]() 这两点之间的距离为半径作弧,两弧交于一点,如图所示,BE即为所求;
这两点之间的距离为半径作弧,两弧交于一点,如图所示,BE即为所求;
(3)CE=CF,
理由如下:∵CD⊥AB,
∴∠FDB=90°,
∵BE平分∠ABC,
∴∠CBF=∠DBF,
∵∠DFB+∠DBF=∠CEB+∠CBF=90°,
∴∠BFD=∠CEB,
∵∠BFD=∠CFE,
∴∠CFE=∠CEF,
∴CE=CF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目