题目内容
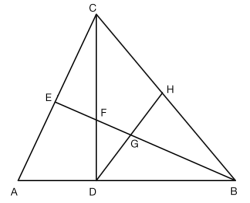
【题目】如图,在△ABC中,BE平分∠ABC,DE∥BC.
(1)判断△DBE是什么三角形,并说明理由;
(2)若F为BE中点,∠ABE=30°,求∠BDF的度数.
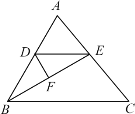
【答案】(1)△DBE是等腰三角形,理由见解析;(2)60°
【解析】
(1)如解图所示,根据角平分线的定义可得∠1=∠2,然后根据平行线的性质可得∠2=∠3,从而得出∠1=∠3,根据等角对等边即可得出结论;
(2)根据三线合一可得DF⊥BE,从而得出∠DFB=90°,然后根据三角形的内角和定理即可求出∠BDF的度数.
解:(1)△DBE是等腰三角形,理由如下.
∵ BE平分∠ABC,
∴ ∠1=∠2.
∵ DE∥BC,
∴ ∠2=∠3.
∴ ∠1=∠3.
∴ DB=DE.
即△DBE是等腰三角形.
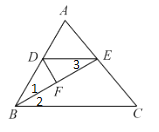
(2)∵ DB=DE,BF=EF.
∴ DF⊥BE,
即∠DFB=90°.
∵∠ABE=30°
∴∠BDF =180°-(∠ABE+∠DFB)=180°-(30°+90°)=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目