Question

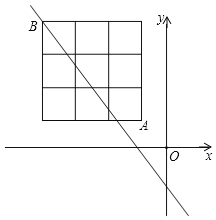
【题目】如图，在Rt△ABC中，BC2，∠BAC30°，斜边AB的两个端点分别在相互垂直的射线OM，ON上滑动，下列结论： ①若C，O两点关于AB对称，则OA；②C，O两点距离的最大值为4；③若AB平分CO，则AB⊥CO；④斜边AB的中点D运动路径的长为.

其中正确的是（ ）

A. ①② B. ①②③ C. ①③④ D. ①②④

Answer 1

【答案】D

【解析】分析：①先根据直角三角形30°的性质和勾股定理分别求AC和AB，由对称的性质可知：AB是OC的垂直平分线，所以
②当OC经过AB的中点E时，OC最大，则C、O两点距离的最大值为4；
③如图2，当∠ABO=30°时，易证四边形OACB是矩形，此时AB与CO互相平分，但所夹锐角为60°，明显不垂直，或者根据四点共圆可知：A、C、B、O四点共圆，则AB为直径，由垂径定理相关推论：平分弦（不是直径）的直径垂直于这条弦，但当这条弦也是直径时，即OC是直径时，AB与OC互相平分，但AB与OC不一定垂直；
④如图3，半径为2，圆心角为90°，根据弧长公式进行计算即可．

详解：在Rt△ABC中,∵

∴

①若C.O两点关于AB对称，如图1，

∴AB是OC的垂直平分线，

则

所以①正确；

②如图1，取AB的中点为E，连接OE、CE，

∵

∴

当OC经过点E时，OC最大，

则C.O两点距离的最大值为4；

所以②正确；

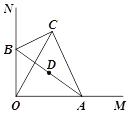
③如图2,当时,

∴四边形AOBC是矩形，

∴AB与OC互相平分，

但AB与OC的夹角为不垂直，

所以③不正确；

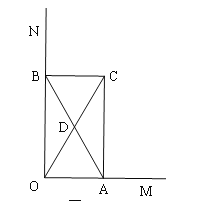
④如图3,斜边AB的中点D运动路径是：以O为圆心,以2为半径的圆周的

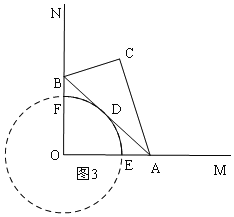
则：

所以④正确；

综上所述，本题正确的有：①②④；

故选D.